最近在 LWN 看到 Theoretical vs. practical cryptography in the kernel 這篇關於 Linux 中隨機數生成機制的討論,原本是想說簡單寫個翻譯,但沒想到為了 trace 原文 patch 改動而跑去看原始碼,發現看不懂之後看到註解裡面提到這個很神奇的論文The Linux Pseudorandom Number Generator Revisited,這是一篇兼具實做但是理論分析相當充實(充實到我都看不懂的那種)的「技術文件」(個人覺得,作為菜鳥看這個比直接去 trace code 學到的東西多一點)
因此以下會從 LWN 那篇文章作為切入點,希望能夠看懂 LWN 那篇文章是在 吵 討論什麼,並且簡單討論一下 Linux 隨機數生成的機制(具體機制有效性證明的部份,儘管論文裡有不少都是在討論這個方向,然而由於個人才疏學淺目前還不會 cover 到那塊)
提昇隨機性的 Linux 補釘
在 Linux 5.8 核心發布以前的一個小補釘 想要解決 TCP 端口分配隨機性不夠,以至於會被猜到的危險
TCP 是傳輸層協議,為了防止其他攻擊者偽造發送者的身份,TCP 要求端口必須要是隨機的,因此我們需要一定程度的隨機性
然而絕大多數電腦程式的執行都是固定的,也就是在輸入固定的時候,我們只會得到固定的輸出
概率本質上依託於隨機性的概念,我們必須要有不可預測且平均分佈的數值才能用來作為概率基礎
你可能會想到像是程式執行時間是一個非常直觀的隨機數值,的確這是一個很重要的發現,事實上現在 Linux 的隨機性來源大多是外部周遭裝置的隨機性,像是硬碟的讀寫速度,鍵盤的輸入速度等等
在 Linux 裡,你可以在 device interrupt handler 那裡註冊,成為隨機性的來源(透過設定 IRQF_SAMPLE_RANDOM flag)
但是現實中,我們對於隨機性的需求頻率遠大於生產速度,也就是隨機性成了供不應求的稀缺資源,我們後面會把量化的隨機性稱作 「熵(Entropy)」(我記得是起源自熱力學的名詞)
於是 Linux 實做中我們能夠接觸到的隨機性(i.e. 用函式庫調用拿到的隨機值)都是「偽隨機數(Pseudo Random Number)」,這些偽隨機數都是利用 Entropy,經過一個固定算法後得到的值,然而這個固定算法通常無法透過回推,從輸出反推回輸入(基本上都是 SHA-1 起跳)
Entropy 內部狀態潛在洩漏的可能性
但是這就是 LWN 這篇文章主要想探討的問題
原始的端口由於也是透過偽隨機數產生器(Pseudo Random Number Generator, 簡稱 PRNG)產生的,其原始的隨機種子(Random seed,原始 Entropy 數丟進去 PRNG 用以產生偽隨機)在沒有改變的情況下容易被反推,並用以預測未來產生的偽隨機數
因此在這個補釘中讓這個生成端口隨機數的函式調用適時的 reseed (更新隨機種子),那麼這些新的隨機種子要去哪裡拿呢?它去拿了「部份的」Entropy,這邊的部份的概念有點 tricky
假設一個 Entropy 大小為 128 bits,它只取前面 32 bits,並用一個類似 CRC-32 的方式 reseed 進原本的狀態
不用 SHA-1 的原因是因為計算成本太高,採用 CRC-32 是為了讓隨機性能更均勻的 mix (後面會提到大量的 mixing function,這是隨機數生成一個很常見的名詞)
但是問題就在於:「如果今天攻擊者能成功拆開 CRC-32,區分開被加進去的部份 Entropy,那他有沒有可能推算出整個 Entropy 目前的狀態?」
如果真的可以推算出 Entropy 整體的狀態,那對於整體系統來說會是一個大災難,(應該是所有的)加密系統會因為「你的隨機(在攻擊者眼裡)不是真正的隨機」而整個失靈
Quick Conclusion: 就短期來說,不會
首先這就是為什麼只拿一部分的 Entropy 出去,這樣可以保證就算部份 Entropy 洩漏也不會危害到整體 Entropy ,另外一部分可能是因為不需要這麼高的隨機性
另外是拿出去的 Entropy 會透過 SHA-1 哈希過才拿出去用,因此還要先過 SHA 這一關
如果你只是想知道 LWN 那篇文章大概在做什麼那大概看到這邊就可以結束了,以下部份會開始著重在 Linux PRNG 的設計
Linux PRNG 簡介
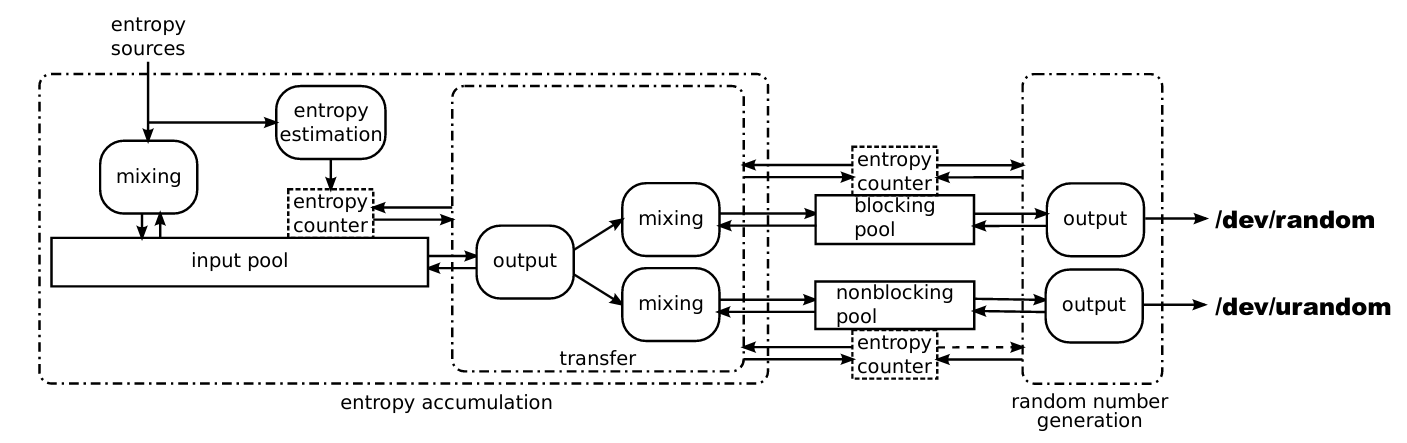
上面這張圖相當重要,可以說是理解 Linux PRNG 的基石
最左邊的 Entropy Source 主要來自週邊硬體,不同硬體有著不同的隨機性等級,這些隨機性會量化成 bit 輸入,透過一個 mixing function 混入底下的 input pool,這個 input pool 本質上就是 Entropy 的匯集池,並且用一個 Entropy Counter 幫所有的 Entropy 匯集池標記其(估計的)隨機性程度,具體理解的話就是水位高低
右邊的 /dev/random 與 /dev/urandom 是兩個 character device,他們提供了 user space 的隨機數需求的介面
一旦用戶向這兩個發送需求,他們會先去檢查各自的 Entropy pool (/dev/random 對應 blocking pool,/dev/urandom 對應 non-blocking pool)還有沒有足夠的隨機性(透過 Entropy counter),可以類比成檢查水池還有沒有可以用的水,有的話直接用,沒有的話向 input pool 發送需求
如果 input pool 有足夠的隨機值(水位)可以轉給 output pool (包含 blocking / non-blocking pool)則透過 transfer 那邊的 mixing function 把隨機性轉出去,但如果 input pool 自己的水位不夠滿足需求,如果是 blocking pool 的需求的話就會等到有足夠隨機性才轉出去,而 non-blocking 則是完全不考慮 input pool 是否有足夠隨機性,反正轉就是了
潛在的惡意 Entropy Source?
Entropy Source
前面提到 Entropy 的來源主要來自周邊硬體,不過就 Linux 來說,由於其目標在提供一個普遍可用的作業系統,因此儘管的確有一些專用周邊硬體用以穩定提供隨機性,這些特殊的隨機性並不會預設為系統隨機性的來源(不過還是可以手動加入)
Linux 系統本身會拿各式各樣的外部中斷產生的隨機性,對於任何外部中斷產生的 Entropy 來說,總共可以量化成三個 32 bits 的數:
輸入數值(與中斷事件有關)
以鍵盤輸入觸發的中斷為例,這邊的值就是鍵盤輸入對應的值
觸發時的 CPU cycle 數
可以理解成高精度的時間記數
觸發時的 jiffies 數
jiffies 表示「從上次重啟 Linux kernel 起算,到觸發中斷為止的 timer 中斷數」,這邊的 timer 中斷頻率可能會隨著設定而不同(大概落在 100 to 1000 ticks 每秒),可以理解成低精度的時間記數
實際上,真正的隨機性會遠小於 32 bits,舉例來說,鍵盤輸入能提供的最大隨機性大概為 8 bits,滑鼠輸入最大為 12 bits,硬碟 3 bits,因此我們還需要評估(盡量悲觀的低估)這些外部硬體中斷到底提供了多少 Entropy
Data injection
然而,如果今天攻擊者透過其他的手段控制了用戶的某些外部裝置,並且用這些裝置註冊作為隨機性輸入,那攻擊者有沒有可能透過把持部份隨機性輸入,或甚至全部的隨機性輸入來達到預知未來隨機數生成的目的?
這就是為什麼 mixing function 非常重要了,mixing function 用以把(可能被攻擊者把持的)隨機性輸入混入現有的 Entropy Pool 並且讓攻擊者依舊不能預測到混合後 Entropy Pool 的狀態
如果你想知道它的數學定義的話:
令 X 為 n bits 的隨機變數,用以表示 entropy pool 的內部狀態,而 I 為 m bits 欲新增的隨機性來源,則 f 為一 function 把 {0, 1}n×{0, 1}m 輸入轉成 {0, 1}n 的輸出;最後 H 代表夏農熵
則 f 必須要滿足以下特性才是 mixing function:
H(f(X, I)) ≥ H(X) and H(f(X, I)) ≥ H(I)
因此選擇一個好的 mixing function 可以保有上述特性非常重要,不過相關的討論涉及到 Twisted Generalized Feedback Shift Register 跟 Galois field 的運算(我之前因為論文想做 network raid 的東西看 RS code(Reed-solomon codes) 碰到 GF,不過之後因為別人做過就棄坑了),個人實在不太敢繼續看下去,如果有興趣的各位可以去看 The Linux Pseudorandom Number Generator Revisited 第 3.1 節
Entropy Estimator
這部份對應到 The Linux Pseudorandom Number Generator Revisited 第 3.2 節,儘管原文提到不少定義細節(還有一些取樣區間的關係,不過我看不太懂)
就我能夠理解的部份,Entropy 的估計主要會「跟前三次的輸入比較得到的最小差值」,並且把這個差值先取個 2 的對數後,bounded 在 0 ~ 11 之間(也就是指如果最小差值大於等於 212,會被限制等於 11)
Output Function
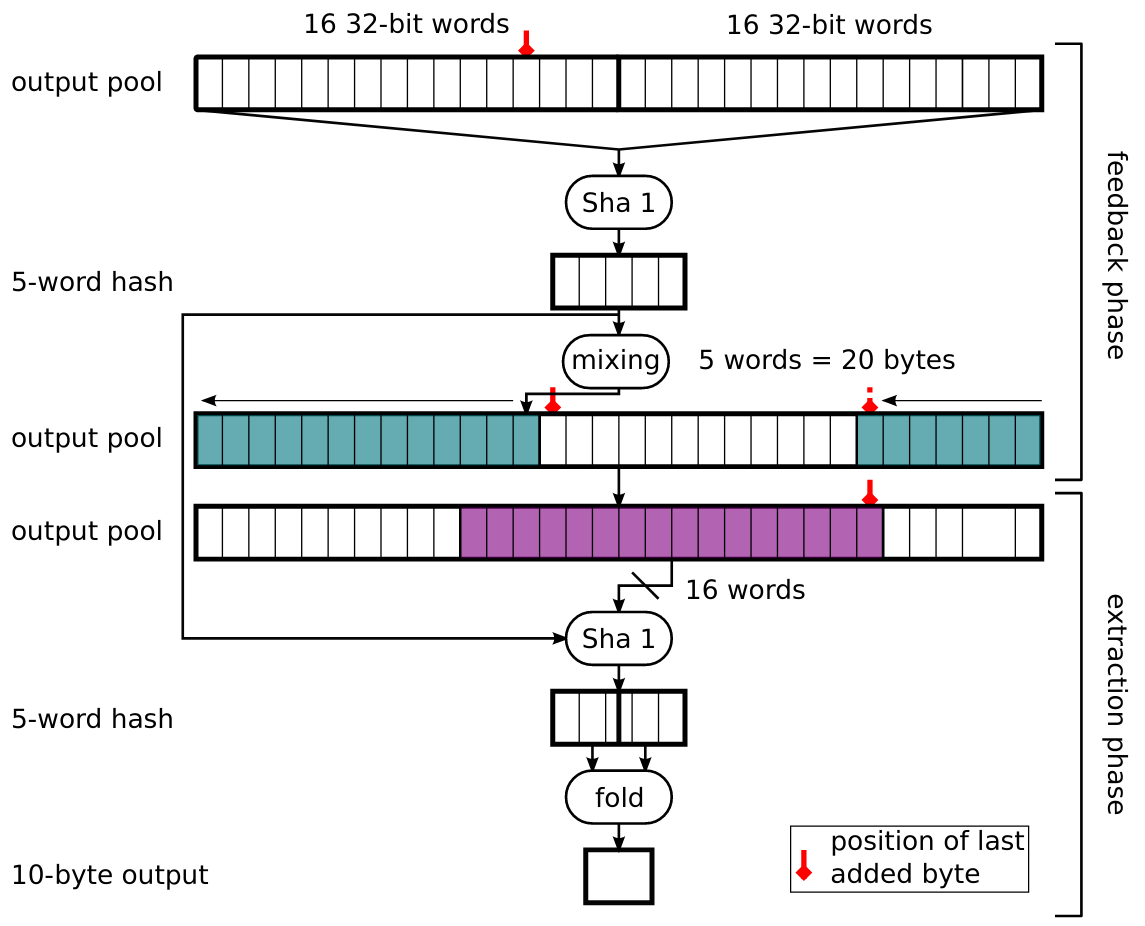
Output Function 是唯一在 Linux PRNG 裡面用到非線性操作的(以我的猜測,它比較昂貴的運算成本導致它只能用在刀口上,像是保護 Input Entropy Pool 的狀態不會洩漏出去),其主要用在兩個場合:entropy 從 input pool 轉送到 output pool 時;外部裝置(如 /dev/random )向 output pool 要求生成偽隨機生成數時
首先整個生成過程涉及到兩個步驟,feedback phase 與 extraction phase
- feedback phase
我們可以看到它一開始會透過 entropy pool 用 SHA-1 生成一個 20 byte 的 immediate result,這個值並不會馬上作為輸出而是會「再一次用 mixing function 混入原本的 entropy pool 中」
關於為啥要混進去我其實也不知道為什麼,我猜測應該是算法為了達到某些特性的要求,不過我也並沒有仔細看這部份的資料
- extraction phase
用 feedback phase 拿到的 immediate result 與 remix 過後的 entropy pool 拿 16 words 出來再做一次 SHA-1,最後把輸出的 20 bytes 做個折疊壓縮(異或 XOR)成 10 bytes
Reference
Secure Random Generators
Understanding random number generators, and their limitations, in Linux
random.c
初探 Linux kernel 亂數產生器 – random generator
The Linux Pseudorandom Number Generator Revisited
後記
之前大學時期印象中 jserv 就有提過 LWN 這個(類似新聞的)網站,主要會講一些電腦科學設計的一些新知,或者是 Linux 設計改動等等,但是由於那個時間沒有這個需要,生活也比較不規律一點因此也沒有想過認真看這些文章
直到最近因為要寫論文做了點實驗,發現實驗跟預期落差有點大,同時也遇到原初設計時沒考慮到的問題,發現自己對實務還是認知過少,前一陣子也聽一場關於高性能所的人打 IO500 榜的心路歷程芸芸,總覺得自己應該要對系統實務有更新的常識觀念,於是索性開始看 LWN 新聞,同時這應該也會是一個相當合適的文章題目來源
不過不得不說,可能是第一次比較認真看這些文章(包含下面的回覆們),有些觀點非常有趣(像是為什麼在上面這個 patch 裡,entropy source 被拿出去 user space 用掉的 entropy 還會被放回去 entropy pool 繼續 mixing,為什麼不能把它移出 entropy source)這些討論需要你對隨機數產生的流程有基本的理解(舉例來說,你需要知道什麼是 mixing function),這導致理解相關背景的時間反而佔據大部分,一旦有基礎的觀念就會比較容易這篇 LWN 文章大概想表示什麼
不過比較可惜的是我還是沒有把 The Linux Pseudorandom Number Generator Revisited 這篇論文看完,主要是它不少需要比較充實的數學基礎才能看懂的數值分析,這部份由於最近在寫論文,也認知道有數學基礎下的分析才比較有意義,因此前一陣子閒暇時也在重新補充數學基礎,不過要看懂這篇論文的數學分析應該還是言之過早