
最近在靠北工程師上面看到這張梗圖,其實我也沒寫過 PHP,不知道那邊狀況怎樣,但是其實浮點數運算這個議題挺廣泛的,也並不侷限於只有 PHP 有這個「問題」,正好之前在 Jserv 老師課堂上有稍微研究一下這個議題也寫了些筆記(我們自己寫的是浮點數運算和定點數操作,老師的講義是你所不知道的 C 語言: 浮點數運算),現在重新整理一下筆記,並且看能不能順便更新一點內容
什麼是浮點數
浮點數(Floating Point Number),就是定點數(Fixed Point Number)的另外一個方向,我們常用的整數 (Integer)就是定點數的一種
定點數,顧名思義,就是小數點固定(或者說小數點後位數固定);而浮點數自然就是「浮動的小數點位置」,你也可以把浮點數看成用科學記號表示的數字,我們可以透過改變 10n 的 n 大小來移動小數點
但是如果只是這樣,並不能解釋為什麼浮點數運算會產生誤差(尤其是我們可以用科學記號正常表示且運算,不會出現誤差)
從理論到工程
從數學的角度來看,我們假設我們是在十進制的世界裡,並且很完美的我們可以有無限的資源表達一個數字,這可能也是為什麼 0.999… 九循環會等於一
但是實際上,在電腦科學的角度,我們無法正確表示「0.9 九循環」的這個概念(至少據我目前所知,不過應該還是可以想辦法弄出一個對應的抽象數值表示法,但是至少我沒看過)
原因也很簡單,資源是有限的︰我們必須用有限的(且適當的)位元數表示一個數字
以 C 語言為例,表達一個數字通常可以用 2 ~ 12 bytes(當然你可以自定義一些有的沒的,但那不在我們這次的討論範圍內),這代表如果今天不考慮負數的整數(也就是 Unsigned Integer),那我們大約可以表示 216 ~ 296,也就是 104 到 1028 數量級之間
聽起來不錯,這範圍挺大的,就算要表示負數也大概只要把範圍縮小一半(誤差取決於設計有沒有正負零),但是那要怎麼表示小數呢?
定點數的優劣
一個最簡單的方法,我們也不用更改數值的表示方法,我們只需要改變我們讀它的方式
舉例來說,以往看到「1024」這個數字我們會假設它的小數點在 4 之後,也就是沒有小數的部份;但是現在我們統一改變我們讀它的方式,我們現在規定「小數點統一在末二三位之間」,於是一瞬間這個數字就變成 10.24 了
聽起來真是一個完美的辦法,簡單而優雅,我們用極致的效率表示數值的完全精度,完全沒有浪費!還會有什麼問題嗎?
很可惜的是:
我要怎麼讀它
假設你今天是這套系統的設計者,你可能可以對整個運作流程瞭若指掌,你知道整體數值系統如何運作,你也很清楚應該怎麼解讀它們;但是假設你是這個新系統的新手,你完全沒有想過原來小數點放在末二位,系統的文件要不是雜亂難懂不然就是根本不存在,會發生這樣的原因就是它本身不是 self-explanatory,這不是一個規格化的數值表示
我想要表示更小 /大 / 精確的數
假設今天我們用的是 C 語言一般的 signed int ,長度是 4 byte,同時也定義小數點是末二三位之間,這代表我們只能表示 21474836.47 ~ -21474836.48 間的數
所以我們不但無法表示這個區間外的數,我們也無法表示 1.024 更高精度的數字(需要捨棄或進位)
好了我們現在知道定點數的缺點了,儘管它能夠很高效的表示數值,但是它的靈活度很低,那我們應該怎麼獲取一個通用的泛用表示法?
別被搞混了,定點數也有它的優勢,儘管在後面會提到浮點數各種缺點,但是這邊簡單講一下定點數的優點
事實上,最近不少研究都把針對浮點數轉換為定點數表示,像是 Making floating point math highly efficient for AI hardware,Applied Machine Learning at Facebook:A Datacenter Infrastructure Perspective, Quantizing deep convolutional networks forefficient inference: A whitepaper
機器學習的優化是一個好場景,由於我們實在不需要表示那些極小趨近零的數(事實上,一個機器學習優化方法就是直接把這些極小數消成零)
同時也不需要表示極大數,這時候用上定點數效率更高,同時也可以減少硬體需求
犧牲位元來表示浮點數
所以浮點數出現了,它有點像是科學記號表示,但是是二進位的 (10…11)2 * 2n,然後無論是前面的常數項 (10…11)2 或是後面的指數 n 都有位數表示限制
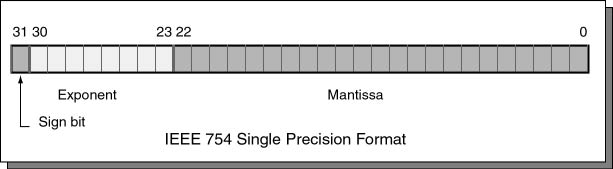
上圖是 IEEE 754 規格書提到的浮點數格式,我們可以看到總共有三個部份:
- 正負號(Sign bit):共一個位元
- 指數 (Exponent): 其實就是代表你要把底數左/右移幾位
- 底數 (Mantissa):這邊比較麻煩的是,它除了是二進位的小數之外(舉例來說,(10.01)2 = (2.25)10),同時 mantissa 的小數點預設在最高位左邊,同時會偷偷在小數點左邊加上一個 1,變成 1.[mantissa] 的型態(這樣做是完全可行的,因為小數中總有一個位元是 1,你只需要透過 Exponent 去位移就好了)
就工程上來說,浮點數必然會出現誤差,舉例來說 (1.1010)2 * 2 2 的浮點數,其等於將(1.1010)2 小數點右移兩位,變成 (110.10)2 ,化成十進位就是 2 2 * 1 + 2 1 * 1 + 2 0 * 0 + 2 -1 * 1 + 2 -2 * 0 = 6.5
我們可以看到,浮點數只能表示用 2 -n 組合出來,這自然會導致有些數轉換後將喪失正確性
浮點數除了表達這些「正常」的數值外,同時也有一些很神奇的數值表達模式
Denormalize mode 與 Normalize mode 間的轉換,像是因為乘法導致 Denormalize 到 Normalize 的這個 實做 挺有趣的,但是因為有點 trivial 就跳過了
Infinity & NaN
浮點數表示法本身就有提供表示「無限 Infinity」與 「NaN(Not a Number)」的表示方法
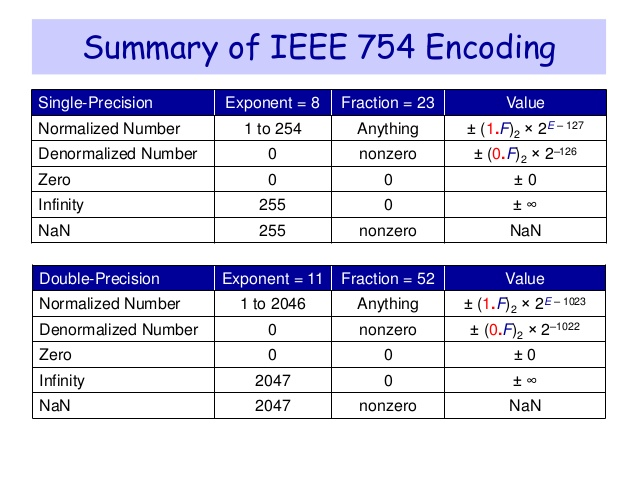
除了無限有分正無限與負無限之外,我想最有趣的部份應該是 NaN 了,NaN 有很多神奇你應該不會想到過得行為
NaN 出現時機最常見的就是除數為零,還有一些等下會提到的案例,但是你知道:
其實 NaN 有兩種嗎?
Quiet NaN & Signal NaN
根據浮點數規格書 IEEE 754 第 6.2 章提到,對於 NaN 來說
- mantissa 起始位元為 1 的話就是 quiet NaN
- 反之 mantissa 起始位元為 0 ,但其餘位置非零的話就是 signal NaN (全部都零會變成無限的表達式)
你可能會想問,這兩個差在哪?
一旦運算產生 Signal NaN,通常 FPU (浮點數處理單元,Floating point Process Unit)會報錯然後你會在執行時期得知;但是對於 Quiet NaN 來說,系統不會主動報錯,你必須自己去檢查運算結果
你可能不太懂這意味著什麼,Signal NaN 是一個討厭鬼,它會在你一出錯的時候跟你講,有可能導致你的程式中斷啥的(這有可能導致部屬中斷的損失),但是 Quiet NaN 更像是一個會傳染的未爆彈,你通常不會意識到它的發生,debug 也並不是那麼容易(畢竟你需要檢查所有有嫌疑的數值),更不友善的是,它會傳播開來(我更喜歡叫它感染)
出現 NaN 的時機們
如果你真的很需要清楚知道這些行為,請翻閱 IEEE 754 7.2 節,那裡有完整的規範說明
因為全部列出來會有點冗,我決定挑幾個比較有趣的:
會產生 Quiet NaN 的
- 涉及到 Quiet NaN 的大部分運算(除了某些 casting)產出都會直接變成 Quiet NaN
- 0 乘 ∞ 或是 ∞ ± ∞(這邊的無限也有自己的正負號)
- 0 除∞ 或是 ∞ / ∞
- 對負數開根號
會產生 Signal NaN 的
- 嘗試對 NaN, infinity, 或是整數表示範圍外的浮點數轉換(casting)成整數
從工程又回到理論
為什麼二進制無法很好的表示小數?
問題在於,為什麼在表達十進制整數的時候,我們明明可以完整的表示;但是一旦到了小數的範圍,就開始產生精度誤差了呢?(有同學表明如果我們可以用無限位元表示小數,則誤差部份就可以展開成一無限項的表示式,也就沒有誤差了)
不過這樣問題就會變成「對於一個有限的十位數整數,我們可以只用有限的位元表示並且不喪失任何精度,但是對於小數來說,無論是否有限,我們都沒辦法用有限的二進制位元表示」

定點數能夠精確(以上圖來說,accurate 但可能不 precise)的原因,以我的理解來說,儘管定點數底層與浮點數一樣,都是二進制構成
但是我們的小數點實際上可以有不同的加法
- 一種是跟浮點數一樣,在二進制的時候加上去,這樣 accuracy 會跟浮點數一樣
- 另外一種是在二進制轉成十進制之後,再加上去,這時候 accuracy 就會是十進制的
一種可能比較好理解的說法是,說白了小數點就是做除法,在二進制裡面加就會變二進制的除法,在十進制裡面就變成十進制的除法
但是這看起來非常不嚴謹阿,我們能用數學方法證明嗎?
這個問題花了我不少時間,不光是思考,問同學,或是補足相關的數學知識等等,我想我只能在這邊提出一個個人的推論(而且不甚嚴謹)
Cardinality 勢 ?
這應該是個錯誤的思考方向,如果急著想知道答案的可以先跳過
不過還是挺建議順著看釐清是哪邊有問題
集合論中有一個很有名的 Cantor’s diagonal argument(感謝數學系大佬莊同學熱心解惑)用來說明實數集與整數集之間「不同勢」,有沒有可能是這個原因呢?
什麼是勢
對於有限大小的集(Set)來說,我們可以很簡單,直覺的比較兩個有限集的大小;但是對於那些無限集呢,像是整數(Integer)或是實數(Real Number)這類有無限大小的集呢?
這時候我們就要用到集合論裡面的「勢(Cardinality)」這個概念了
對於無限集(儘管有限集也具有勢,但是那不是我們主要討論的目標)來說,我們可以透過比較他們的勢來作到比大小的目的
由於無限集不可類舉,所以我們這邊需要找的是這兩個無限集間的映對關係,假如存在 B → A 的單射,則定義集合 A 的勢大於集合 B;但是如果兩者完美一一對應,則我們稱之為等勢
有沒有可能找不到這個對應關係?
有,但是那代表你需要證明這個關係不存在(通常都會存在這樣的對應關係,至少反正 CS 領域應該都是用現成的)
那有沒有可能不只 A 有一些無法被對應到的元素,B 也有一些?這樣誰比較大?
有,那代表你的對應關係找得很爛,請找一個比較好用,容易比較的
簡單舉個例子好了,令 αi = {1, 2, 3, …..} 的一個無限正整數數列,我們可以構造另外一個數列 βi = {2, 4, 6, …..} 其中 β 內每一個元素都正好是 α 的兩倍,這樣的對應關係是一對一的,儘管我們大概可以感覺到 α 應該會大於 β (畢竟 β 有的元素 α 都有)
但是因為根據勢的定義
- 這兩個都是無限數列
- 存在一對一的對應關係(或叫做滿射?)
我們會因此定義這兩個集合等勢
好了,現在我們知道勢的基本觀念了(而且那也是我們目前只需要懂的),現在回到二進制表示的問題
我們已知有限的二進制位元能夠完美的表示整數域的一部分數字,也就是說他們具有「等勢」,但是「整數」與「實數」有等勢嗎?
Cantor’s diagonal argument
要證明某些集是不是跟整數集等勢,常見的作法是看那些集是不是「可數集」,因為一旦是可數的,這就代表我們可以把整數用索引(index)的方式對應到那些可數集上了
相關的常見範例像是「自然數與有理數」可以直接看連結的影片(Integers & Rationals are both infinite but is it the SAME infinity?)
其實關於 Cantor’s diagonal argument 也有相關的介紹影片,但是這邊還是簡單講一下
Cantor’s diagonal argument 主要的想法就是要說明實數域實際上是不可數的,這會透過憑空生成一個完全不在列舉項但又完全合法的「不存在的實數」達成
舉例來說,我們今天嘗試對所有的小數列舉:
- α1 = 0.12345…
- α2 = 0.24680…
- α3 = 0.01010…
順序是什麼並不重要,後續位元省略,重點是我們「假設我們可以窮舉出所有項,也就是所有實數都應該有自己的索引」
但是在這些被「窮舉」的數字中,我們可以透過取出每項的一個位元(第一項取第一個,第二項第二個,以此類推)組合成一個新的數字,並且這個數字並不在我們窮舉的清單上,所以我們反證得實數集不可數

恭喜!因為實數域跟整數域不等勢,所以不能夠用二進制轉換!
真的是這樣嗎?
以上的證明主要針對無限數集,我們也可以很直覺的得知某些無限數集明顯大於其他「雖然等勢」的無限數集(像是 2N vs N)
但是浮點數能夠表達無限小數嗎?浮點數到底想表示什麼?
浮點數只能表示有限小數
沒有錯,因為我們只有有限位元,除非我們專門想出一個用於表示無限位元的運算系統,不然浮點數能夠處理的永遠都只有有限數集(所以表達無理數或者是一些循環小數本質上就不可能)
扯一下關於無限小數的題外話,其實 [0, 1] 間的實數表達方式不唯一,舉例來說,0.1 其實也可以表示成 0.0999… 九循環,不過因為浮點數不能表示無限小數,所以這邊就可以忽略掉了
不過這樣不就矛盾了嗎?前面已經證明有理數與正整數是等勢,所以這不就代表我們應該能夠用二進制完美表示小數嗎?
Divide and Conquer
我們再次回到進制的根本上,對一個十進制整數轉換成二進制的過程,基本上可以看成不斷除以二的過程,也就是一個 2 次方展開的過程,也就是我們不斷嘗試用更小的 2 次方去組合成一個大的整數;在這個過程中,2 次方的最小組合單元是 20 = 1 是一個確定的數(也剛好十進制的基底跟二進制的基底都一樣),因此我們可以完整的在這兩種進制間轉換
但是情況換到小數就是另外一回事了,我們找不到小數的表示基底(因為我們只有有限位元),這就有點像是限制你不用 20,21 等等去表示一個整數,這會自然產生精度誤差
那整數跟小數到底有什麼本質上的差異,導致小數無法找到基底呢?以我個人粗淺的理解,應該是因為 20 與 100 交匯在 1 這個無法表示小數的數值上,導致大於 1 的整數可以收束在 1 這個最小整數基底上,但小數部份因為沒有共同基底導致開始分家
後記
我本來寫這篇文章是想說順便複習 NaN ,Denormalized mode 那些有的沒的,但是沒想到中途蹦出那個「為什麼用二進制表達小數會有誤差」的問題之後就徹底歪了,算是徹徹底底繞了組合論那邊一圈才發現好像不是勢那邊的問題,問題的根本原因好像就是一開始提到的,「因為我們沒有無限位元表示小數」
寫的其實心也挺累的,本來想在勢那邊就打住,裝死假裝沒有想到後續的問題,但是總還是覺得哪裡怪怪的,覺得不能說服自己的話不如不要寫
不過就算是最後的這個小結論,感覺也沒有太多的 insight,不過我覺得這應該是我還太淺了;本來想說可以用什麼數學定理去證明的,或至少比較有說服力的說明,不過看起來是失敗了
希望有大神可以解釋的更清楚一點,或者給出一個比較嚴謹的說明