Peek into Gurobi, a mathematical solver

Gurobi 是一個數學規劃工具，用於解線性規劃 (Linear Programming) 或是二次規劃（Quadratic Programming）

使用者首先需要將應用場景以數學描述抽象化（成一次方程式或最多二次方程式），隨後 Gurobi 會根據給定的目標以及條件找出最符合需求的解（如果解存在的話）

值得注意的是，電腦科學中不少優化方法都是 non-deterministic 的，以機器學習來說就是 local minimum 與 global minimum 的差異，但是線性規劃是一種確定性的最佳解（再重申一次，前提是要有解）

儘管線性規劃乍看之下非常相似國中小學習解方程式組的過程，但是就跟論文研究一樣，從廣到深能夠探討研究的東西還真的不少，並且也需要考慮到「理論與實做的差距」這個老問題

以下我會從線性規劃（儘管 Gurobi 能夠支援二次規劃，但是本文不打算討論到那個部份）的背景簡單帶入，

線性規劃背景

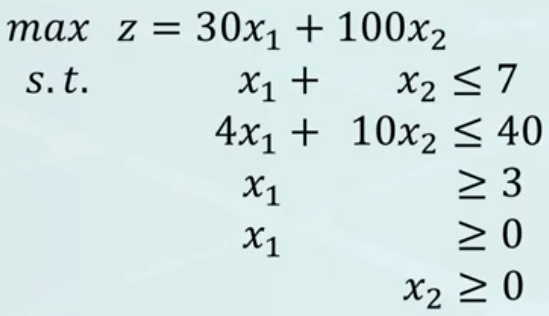
我假設大家應該都學過國中小的解方程組，並且知道怎麼用數學式去表示給定問題，那麼大家應該就會對上圖不陌生

第一行表示「目標函式（Object function）」，通常是最大/最小化某個數學多項式，假設這邊的 30 X₁ + 100 X₂ 代表一個售價 30 元的貨物 X₁個與售價 100 元的貨物 X₂個的總和收益最大化

那麼第二式以後的就是這個數學規劃的「約束（Constraint）」，也就是必須符合的條件

我們國中小的數學老師通常都會教我們用圖解，首先這些約束必須產生一個有限的收斂平面（Bounded），因為老師告訴我們解必然出現在約束的交點上，因此我們可以用目標函式去逼近找出會產出最大值的頂點

那現實中的線性規劃是這麼做的嗎？

線性規劃實現

大多不是的（儘管 Simplex 算法概念上很接近，但是它至少在每次迭代有想辦法往正確的解方向前進，作為一種優化），因為擴展性太差了

以 Linear Programs, sec 3.3.3 裡面提到的，假設今天總共有 M 個約束條件，而一個頂點由兩個以上的約束交集形成，那麼我們實際上可能需要找 C^M_N 個選項，也就是 M! / (N!(M-N)! ) 種，這樣的運算時間複雜度實在太大了，這也就代表我們不可能透過純粹暴力法的方式解決

為了解決這個問題，我們可以引入對偶問題（Duality）的概念：

什麼是對偶問題？

一個線性規劃的問題可以被形式化成：

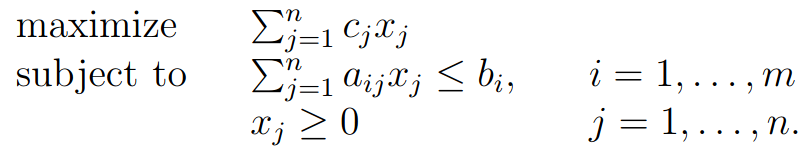
我們以 Linear Programs, sec 1.2 裡的例子來說明，我們假設今天我們是原油提煉廠，眾所周知高中化學告訴我們石油原油是多種有機化合物組合的混合物，因此我們今天想透過從上游進貨，提煉原油並加工得到石化材料販售

我們假設 X_j 是第 j 個產品的產量，而 b_i 代表第 i 個材料的存量，a_ij 則代表把材料轉換成產品的比例，也就是一單位的產品需要多少材料，最後 c_j 代表第 j 個產品的每單位售價

今天作為老闆，我們當然是希望收益盡可能高，在成本不變的前提下，當然是最大化產品販賣所得

但是有沒有可能我今天把產品拿去賣的收益，反而比我直接把材料賣出去的獲利還要低呢？這個時候我們就可以換到對偶問題去看看了

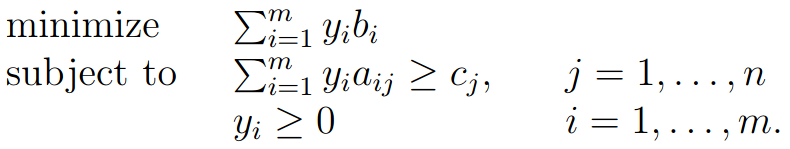
問題的變數從原本的 X_j，也就是「第 j 個產品的產量」變成 Y_i，「第 i 個材料的進價」，而其餘數值的意義與原本一樣

需要非常注意的是下標 i 主要表示產品端的，而 j 主要用來代表原料端的

另外「其他數值語意一樣」這件事是必然的，在後面我們會提到我們可以直接從原始問題（Primal problem）推出對偶問題（Dual problem）

我們的問題從原本的「賣產品」變成「賣材料」，首先看到約束條件，因為我們想探討虧錢的狀況，也就是產品售價低於材料進價，因此 Y_i a_ij 表示把產品拿去當材料賣能得到的錢，而 c_j < Y_i a_ij 就代表售價定的不大於進價

最後我們的目標語意跟原始問題一樣，不過在對偶問題裡我們不能控制產品產量，只能控制材料進價（我們想知道什麼樣的材料價格我們是虧的），因此目標是讓成本最小

原文在這邊有點草草帶過的意思，我根據我的理解做了一點應該算不小的語意改動（像是目標函式為什麼從最大化變成最小化，儘管後續的講解會用另外一個角度講解這是必然的，但是這邊要怎麼具體應用在現實語意還是需要思考的）

其實對偶問題在博奕論裡也有用到，之前跟同學討論到德州撲克的最佳策略時有位姚班的同學講到（不過我實在聽不懂），Stanford 的筆記似乎也有提到（不過我還沒看到，Stanford 筆記的數學特別多看起來特別累）

我們把原本的賣產品的問題叫做 Primal Problem，並把後面買材料的部份稱為 Duel Problem；但是為什麼我們好好的 Primal Problem 問題不用，要故意轉換成 Duel Problem 自討苦吃？

Weak Duality

感謝 Operations Research 05C: Weak Duality & Strong Duality 平易近人的講解，想要看影片的可以花不到十分鐘去看看，以下的討論也是基於這部影片的

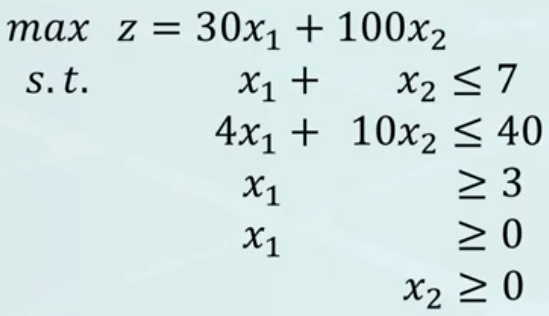
現在我們回到原本比較具體的數學描述，我們定義上面這個線性規劃的目標 z 的最大值為 z^*，然後我們來探討一下「z^* 的可行範圍」

對於所有符合約束的 x₁, x₂ 帶入目標函式都會小於 z^*

這是因為根據定義，z^* 就是目標 z 的最大值；因此我們可以在這邊找到 z^* 的下界

那上界呢？
對偶問題的所有可行解，都會是原始問題 z^* 的上界

今天我們要找的是「z^* 的上界」，也就是說這些（畢竟沒有說是最小上界）上界必然要大於所有 z 的可行解，也就是原始問題的目標
好那我們今天來建構一個一定會大於原始問題目標的另外一個（對偶）問題

這部份也可以參考 Operations Research 05B: Primal & Dual Problems
1. 把原始問題的條件整理一下，讓條件運算元全部都變成 LHS <= RHS
  
  把符號不一樣的變號互換位置就好了
2. 調整各約束的係數，讓他們 係數和 對齊目標函數的係數
3. 然後把所有約束加起來，RHS 就會是一種上界

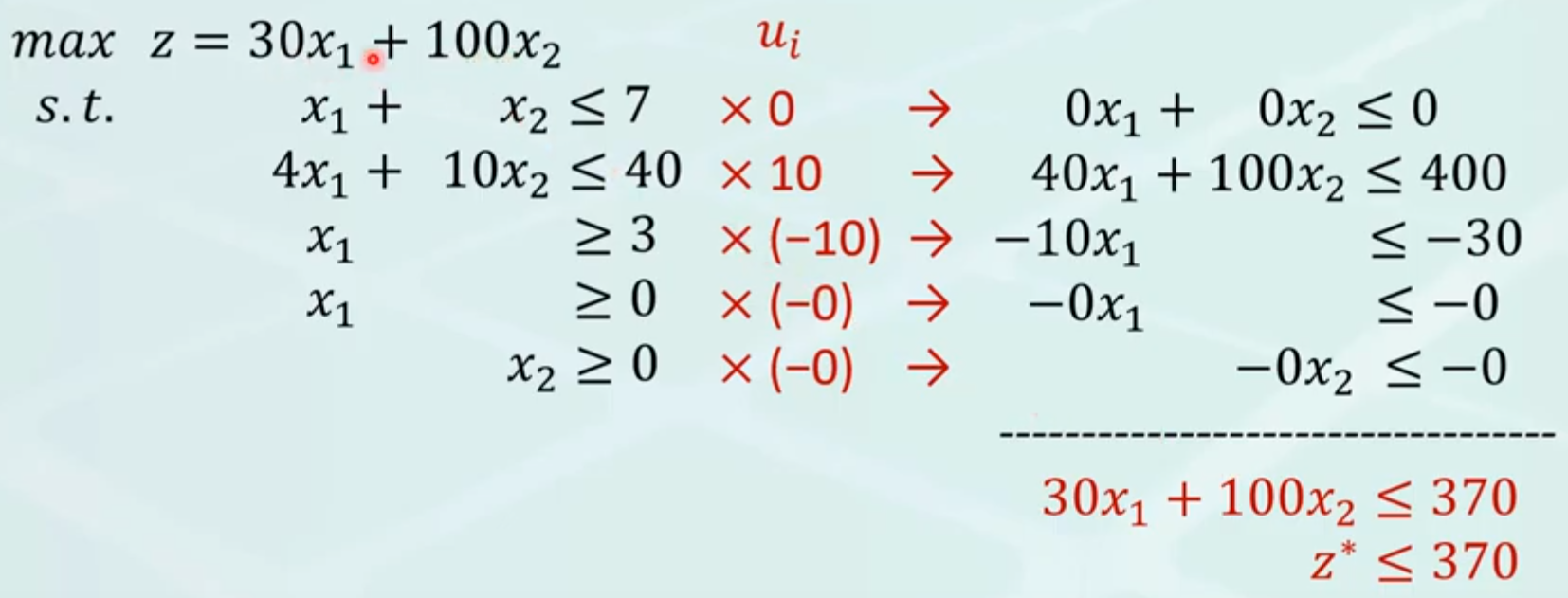
但是實際上，第二個步驟「調整係數以對齊目標」有非常多可行的調整方式，因此這邊應該每個約束各用一個變數 u_k, k = 1,2 ,3, 4, 5

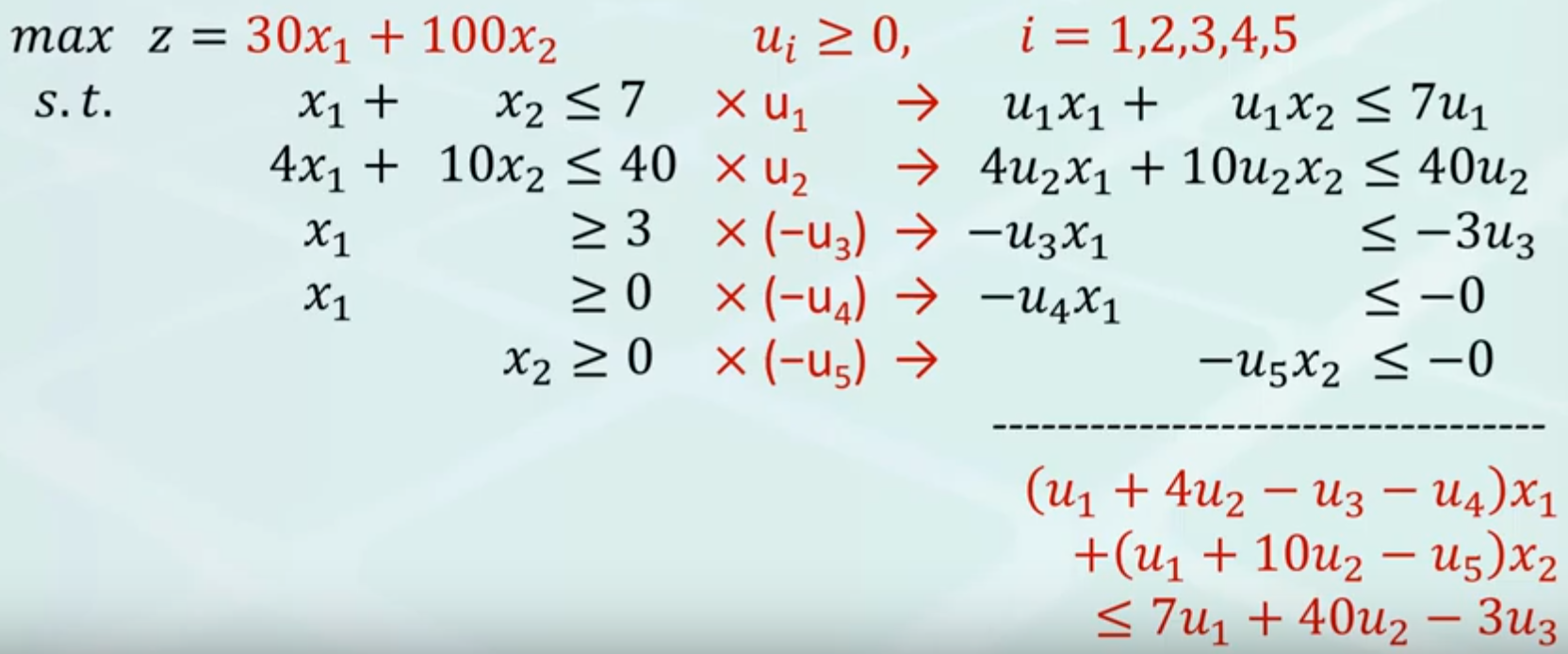
首先，(u₁ + 4 u₂ - u₃) x₁ 對齊 30 x₁，然後 (u₁ + 10 u₂ - u₅) x₂ 對齊 100 x₂

因此原式

(u₁ + 4 u₂ - u₃) x + (u₁ + 10 u₂ - u₅) x₂ = 30 x₁ + 100 x₂ = z <= 7 u₁ + 40 u₂ - 3 u₃

我們原始的目標是「最大化 z」，但是從上式可以看到 z <= 7 u₁ + 40 u₂ - 3 u₃，我們因此知道 7 u₁ + 40 u₂ - 3 u₃ 這東西總是大於等於 z，因此要找「最大的 z」就等於找「最小的 7 u₁ + 40 u₂ - 3 u₃」

我們於是可以透過上述一系列操作把一個 Primal problem 轉換成它的 Dual problem，並且 Dual problem 的解永遠不小於 Primal problem 的解

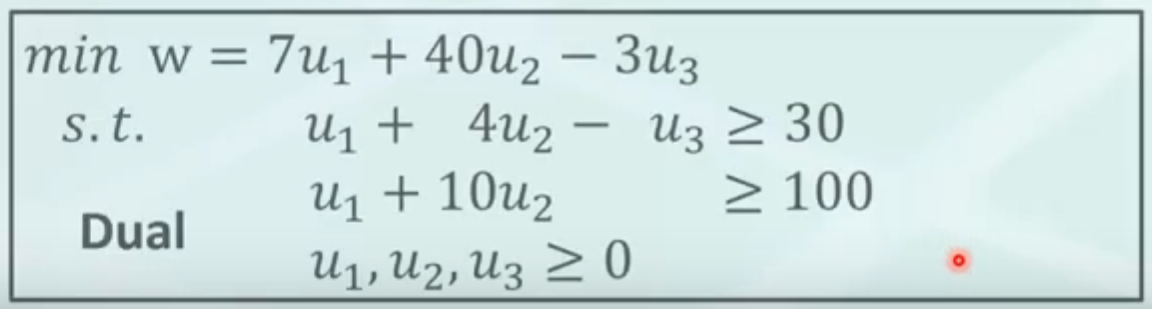
事實上，Dual problem 可以更精簡成上圖，由於原本的 u₄, u₅ 都只有出現在一個約束中，這個時候可以把這些多餘的變數去掉並且把等號改成不大於

Strong Duality

好了我們現在已經知道 z^* 的下界會落在 Primal Problem 裡，而上界會落在 Dual Problem 裡，但是我們需要的是 z^* 的確定值不是一個區間阿

Strong Duality 告訴我們：「只要你能夠在 primal problem 與 dual problem 各找到一組解，使得其目標值相同，那麼這個這個目標值就是最佳解」

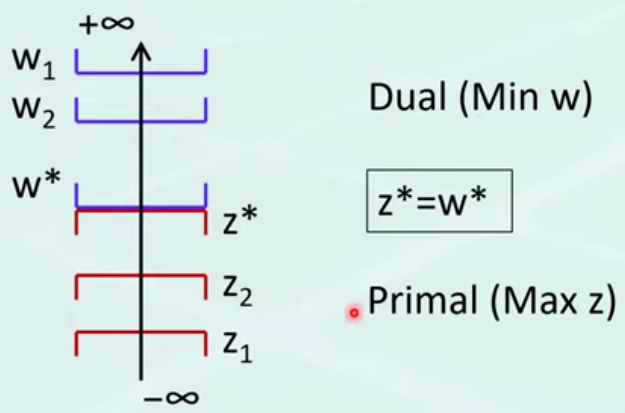
也就是說，Primal Problem 與 Dual problem 共用一個最佳解（Primal Problem 的最大目標值，同時也是 Dual Problem 的最小目標值），因此可喜可賀的是，一旦我們在兩個問題中找到同樣的目標值，我們就可以宣告我們找到問題的答案了（而不需要迭代過所有的可行解）

實做演算法

這部份要入門推薦先從 LP Algorithms, and Seidel’s Algorithm 開始看，它幾乎沒有太難懂的理論，但是並沒有提到對偶問題的部份；而 Algorithms, illinois 則提到 Simplex 算法在 Primal & Dual 上的 pseudo code

Simplex
Operations Research 05E: Dual Simplex Method
Ellipsoid

Again, CMU 有著相當棒的線上資源 The Ellipsoid Algorithm || @ CMU || Lecture 19a of CS Theory Toolkit，根據影片的上傳日期我猜是因為疫情所以也是用網路上課

參考資料

這些課程網站通常可以從 URL 的巢狀結構推斷出課程文件的部屬，像是可以往上找課程本體，或者在某些網站在某些節點不給存取時，順著文件名平行增減做一點人工爬蟲還是挺方便的

好了，偏理論的背景前情提要結束了，以下才是關於 Gurobi 實做

Gurobi

Gurobi 直接提供一個算線性規劃的工具（一般來說要錢，但是學生可以用學術信箱免費註冊，這可能也是為什麼不少論文都是採用這個工具），而且用了 Gurobi 之後你就不需要考慮要怎麼計算你的線性規劃模型了，你可以直接丟給 Gurobi 來算

Gurobi 輸出

我們可以從 Gurobi 運算結束後最後的輸出結果，瞥見一些純理論不會討論到的實做細節

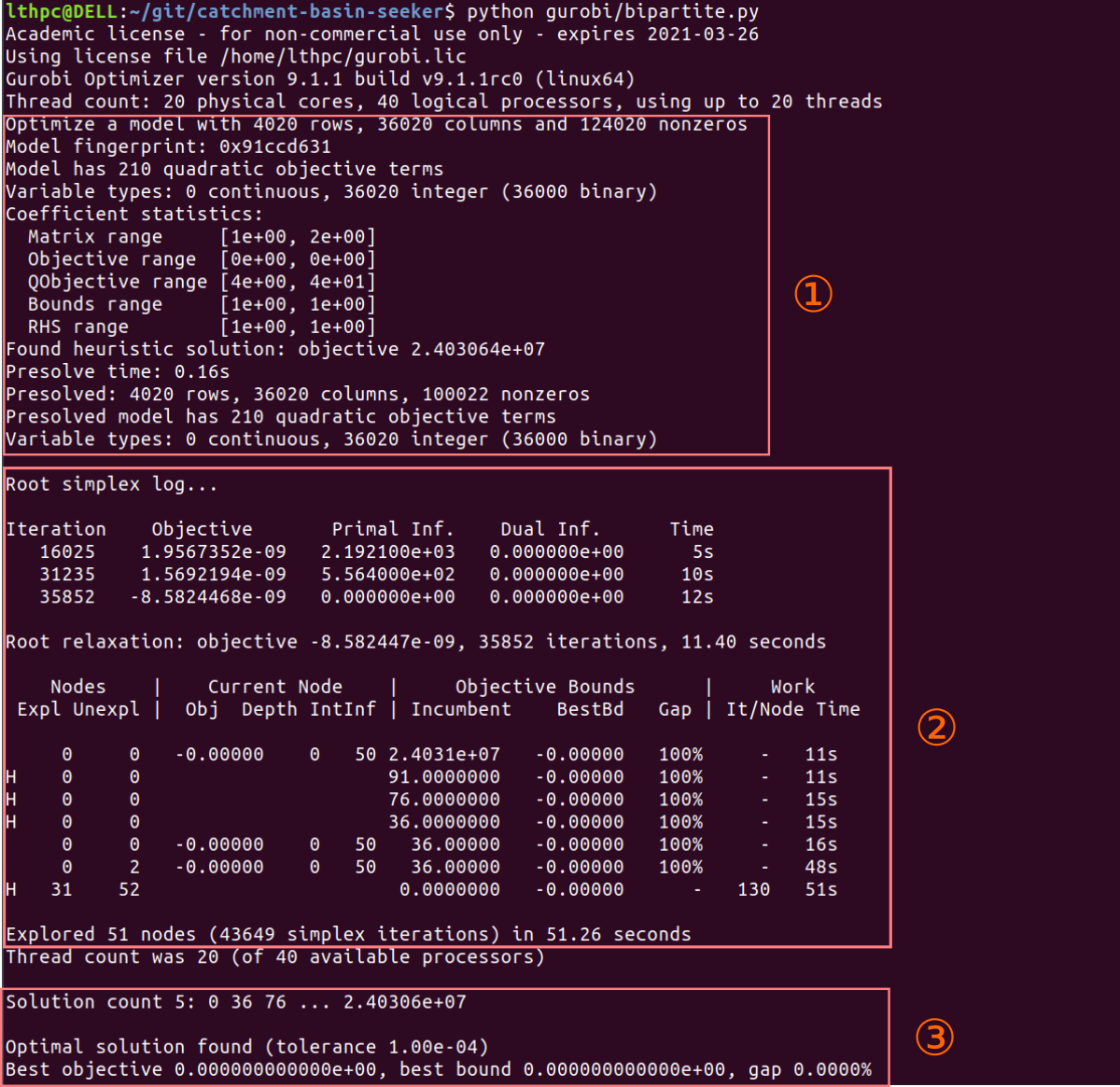
以下討論到的部份，讀者有興趣可以去看 Guidelines for Numerical Issues，但是我覺得它整體讀起來有點像是 FAQ，觀念有點跳，有一些前因後果隔的挺遠，中間還混了一些操作細節，讓人有點容易混淆

簡單來講，線性規劃求解器在實做上有更多的侷限性，而這些侷限大多來自（浮點數）數值表現上有限的精度，正如前面 CMU 線上關於 Ellipsoid 解法講解中涉及到一個非常大的影響因素，也就是可用的表示位元，假設我們只用 8 bits 表示小數，舉例令 (0x1)₂ = 1 / 2⁸ = (0.00390625)₁₀，(0x2)₂ = (0.0078125)₁₀，則我們不僅無法精確表示 0.00390625 ~ 0.0078125 區間中的任何數值，同時對於任何小於 0.00390625 的浮點數我們就只能把它當作零了

有鑑於現實世界中數值表示有它的精度限制，我們需要改變原本理論討論中問題的描述，給出一個更為「工程」的定義

打個預防針一下：我用 Gurobi 也挺斷斷續續的，而且作為初學者的理解應該非常容易錯誤，因此儘管我盡量寫的保守一點，但是如果還是有寫錯的地方，希望大家能夠斧正

上圖是我自己的模型跑出來的輸出結果，我的話會把過程分成三個部份，分別是： ① 模型分析與前處理，② 模型求解，以及 ③ 結果

模型性質以及前處理

從上圖第一部份我們可以看到 Gurobi 會把參數矩陣（主要是約束條件）做一個比較量化的分析，像是：

...
# 因為我採用 Jain's Fairness Index 作為 Obj function 因此目標函數的參數都是 Quadratic 的
Model has 210 quadratic objective terms
# 因為我主要是用 Bool（在 Gurobi 裡叫做 Binary）表示二分圖的 edges，所以絕大多數的變數都是 Bool 型別的
Variable types: 0 continuous, 36020 integer (36000 binary)
# 由於我用來表示二分圖的約束係數數值範圍可以保持差不多一個數量級內，因此沒有什麼問題
# 但是實際上，這部份相當重要，係數範圍調整不好是有可能影響最終運算結果的
Coefficient statistics:
	Matrix range ...
	Objective range ...
	...
# 因為我之前已經算過一次這個模型了，看起來它會把之前跑過的模型做個緩存
Found heuristic solution: objective ...
# 這邊的 Presolve 就我的理解來說，類似編譯器的優化 pass，會先嘗試把模型變成比較好算的形式，不過看起來它好像不能夠太好的優化我的模型（有可能是我的新手模型寫太爛了）
Presolve time: ...
Presolved: ...
Presolved model has ...

我以下會主要放在 Coefficient statistics 相關的講解，而不會提到 Presolve 的部份，因此會忽略第二以及第三部份（第二部份是不可控的算法推進，如果可控的第一部份有做好，那麼後續的就不會有問題了）

Tolerances

在浮點數的世界裡，直接拿去比「等不等於」是一件很不明智的事

1 2	>>> 0.1 + 0.2 == 0.3 False

這個問題要牽扯到浮點數運算，有興趣的可以去看我的另外一篇文章Dive into floating point expressions

比較常用的作法是弄一個 epsilon 做容忍值

1
2
3

>>> epsilon = 0.05
>>> abs(0.1+0.2-0.3) < epsilon
True

Gurobi 也是採用了一樣的作法在 Constraint, Dual Constraint, 還有「判斷結果的變數到底是不是一個整數」上（像是 abs(x-math.floor(x)) < epsilon）

但是比較尷尬的是，這些在 Gurobi 中預設的容忍值都是定值，儘管使用者可以手動調整，不過 Gurobi 還是建議使用者把約束的參數調整到適合的範圍（約束的 RHS 在 10⁴ 量級以內，係數 10^-3 ~ 10⁶，目標函式的可能解在 1~10⁴ 之間）

會針對目標函數的參數設上下限是因為 Gurobi 利用 Dual problem 去判斷這個解是不是最佳解

另外容忍值的引入也可能導致一個理論上不可解的模型，在這些「容忍值產生的灰色區域」上有解

Coefficient rescaling

正如前面所說，為了達到合適的參數區間，我們可能會需要調整各項約束的參數區間讓他們盡可能落在類似的量級

因此 Gurobi 提供一個實驗 ~~（怎麼透過亂調參數達到弄爆模型）~~ 以及其結果可以去 Why scaling and geometry is relevant 看看，它透過「隨機縮放不同約束參數」（像是讓約束 A 的參數全部變一千倍，但是約束 B 的減小一千倍）來讓一個原本有解的模型變成無解

另外 rescaling 可以從兩方面下手：row rescaling / column rescaling ，一個是把整個約束的參數同時縮放，另外一個就是針對所有同一個變數的參數縮放（例如 3x+y<6; 4x+3y<18可以縮放成 0.3x+y<6; 0.4x+3y<18，這樣做就等價成我們換了 x 的單位）

Inevitable large/small coefficients

雖然前面提到我們希望盡可能透過 rescaling 把參數範圍調整到 Gurobi 喜歡的範圍，但是有可能最後事不可為，最後還是會有一些特別大 / 小導致無法表示的值

以 Avoid hiding large coefficients 的例子為例

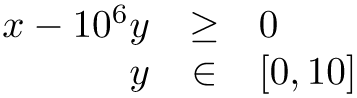
以上圖這個例子而言，10⁶ 是一個不能透過 row rescaling 減小參數範圍的數值，不過為了避開這個數值範圍過大的問題，一些人可能想到用以下的 work-around 替代原本的約束

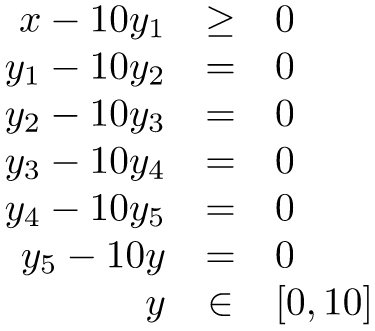
但是這麼做並不會緩解容忍值帶來的灰色區域問題，舉例來說：y = -10^-6, x = -1 可能還會是一個可行解（儘管我們要求 y>0，但是我們事實上能夠接受在容忍度內的極小負值，而這個極小負值會在約束中被那個大參數 10⁶放大到可視的程度）

因此這邊還是透過了 column rescaling 把 y 的單位調整了一下

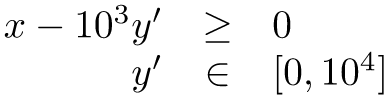
透過調整單位讓整體參數範圍保持在可接受的範圍內

Instability

模型的穩定度也是相當重要的一環，我們希望最終的結果（也就是約束的交點）能夠不隨著約束參數的細小波動（還記得前面提到的容忍值嗎？）而有著劇烈的變化

這也是當代研究線性規劃一個挺主流的課題，比較詳盡的數學解釋可以看 The case of linear systems:，不過根據 Gurobi 的說法，通常來說透過 rescaling 把參數範圍減小到一個合適的大小就比較不容易有問題

Epsilon-optimal solutions

如果目標函式的某項係數非常小，小到容忍值的偏差能夠產生足夠大的影響，那麼解的穩定性也會因此受到影響；以 Dealing with epsilon-optimal solutions 的例子來說：

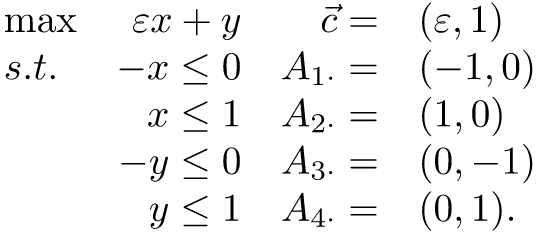
其中 ε 是一個非常小的參數

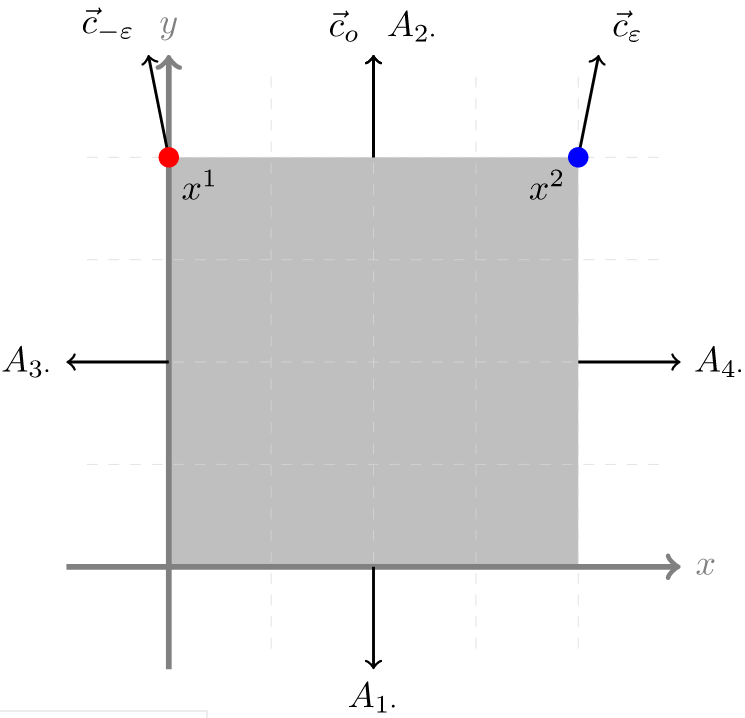
從上圖可以看到 ε ± tolerence 會導致代表目標函式的向量產生巨大的波動，因此在可行解域裡 x¹ 與 x² 都會變成潛在的最佳解

放大一點來看，如果今天可行解域 x 的範圍延伸至更大，放大了 x¹ 與 x² 間的距離，那麼也意味著我們的解將更不穩定

追根究底而言，有兩個因素導致 Epsilon-optimal solutions，一是比較難以避免的「目標函式的偏移方向與某約束近乎平行」，二則是「過大的可行解域」； Gurobi 提到由於前者情形往往難以規避，因此建議大家還是盡量透過 rescaling 取得一個比較小範圍的變數可行域

Thin feasible regions

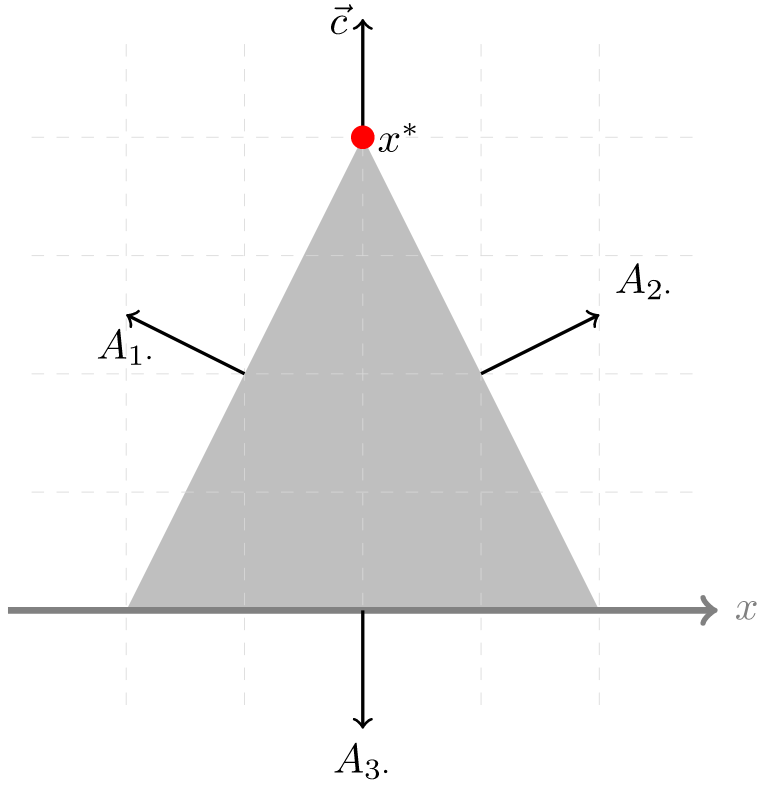
過窄的可行解域（可以理解成一個細長的矩形，或者正確來說「寬極小，但極高的梯形」）也會導致解的不穩定性，同樣也是舉了個 Thin feasible regions 的例子

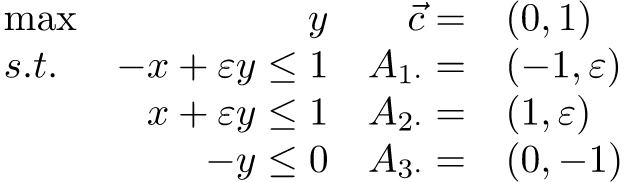
可以看到前面兩個約束去掉 ε 這個 y 項係數的影響後可以說是完全平行的，如果說容忍值的量級不小於 ε ，則容忍值帶來的誤差將會被嚴重放大

後記

原本一開始寫的時候只想考慮 Gurobi 文件裡提到的那些數值問題，因此想說大概花個一兩週的閒暇時間應該是可以整理好；但是讀過第一次之後才發現其實線性規劃有不少背景知識（舉例來說對偶問題），同時線性規劃問題的求解在國外大學 CS 演算法課堂上似乎也是一個 must-do（一想到成大電機可悲的相關課程就實在滿紙辛酸淚）

不過比較可惜的是，我並沒有繼續深入理解這些背景知識，我目前比較傾向於先留個紀錄，如果未來有需要繼續這方面的研究也可以從中間開始切入